Inside Generative Engines:
A Mathematical and System-Level Breakdown
Generative engines like ChatGPT, Perplexity, and Gemini are rapidly replacing search engines, yet few understand how they actually compute an answer.
This post breaks down the generative engine (GE) pipeline as a formal system, from query reformulation to synthesis, and derives the math behind its visibility and optimization behavior.
The Mathematical Foundations of Generative AI
1. The Generative Engine as a Function
At its core, a generative engine is a mapping from a user query to a response:
fGE: (qu, PU) → r
where qu is the user's query, PU is the personalization context (such as location or intent history), and r is the generated response (structured text with inline citations).
Unlike a classical search engine that ranks documents, a GE synthesizes an answer by reading, reasoning, and rewriting through multiple neural modules.
2. The Multi-Model Pipeline
A modern GE is a composition of specialized subsystems:
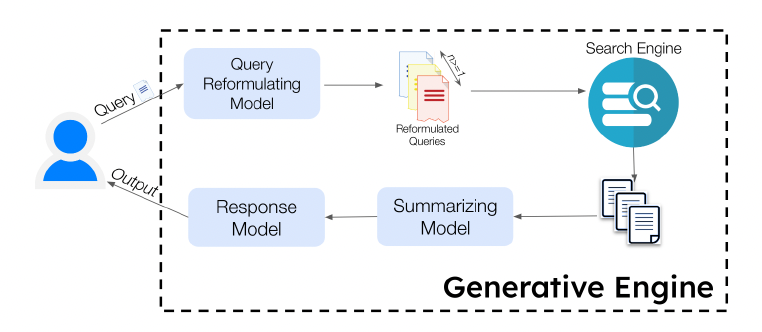
fGE = Gresp ∘ Gsum ∘ SE ∘ Gqr
2.1 Query Reformulation (Gqr)
Expands qu into semantically diverse sub-queries:
Q1 = {q1, q2, …, qn} ∼ p(Q1 | qu; θqr)
Each qi represents a decomposed intent of the original query.
2.2 Retrieval Engine (SE)
Fetches a ranked set of sources using information retrieval:
S = {s1, s2, …, sm} ∼ p(S | Q1; θret)
2.3 Summarization Model (Gsum)
Compresses each document into a short, citation-ready summary using automatic summarization:
Sumj = Gsum(sj), αj = |Sumj| / |sj|
2.4 Response Synthesizer (Gresp)
Constructs the final response:
r = Gresp(qu, Sum)
Each factual unit in r is grounded in the retrieved sources through inline citations.
3. Sentence-Level Structure and Citations
Let the response be a sequence of o sentences:
r = ⟨ℓ1, ℓ2, …, ℓo⟩
Each sentence ℓt is annotated with a citation set Ct ⊆ S.
For attribution integrity:
- Citation precision is the fraction of citations that truly support ℓt.
- Citation recall is the fraction of factual claims in ℓt that are cited.
An ideal generative engine maximizes both.
4. Quantifying Visibility Inside a Generative Response
Visibility in a generative engine is embedded within the synthesized text. It is not defined by rank but by where and how much a source contributes to the generated answer.
4.1 Word-Share Impression
Impwc(ci, r) = (Σs∈S_ci |s|) / (Σs∈S_r |s|)
where Sci is the set of sentences citing ci and |s| is the number of words in s.
4.2 Position-Weighted Impression
To model attention decay across sentences:
Imppwc(ci, r) = (Σs∈S_ci |s| · e-pos(s)/|S|) / (Σs∈S_r |s|)
This approximates reading probability as a function of position in the generated text.
4.3 Subjective Impression
LLM-based evaluators score each citation across six dimensions:
Subj(ci) = [Rel, Inf, Uniq, Pos, Click, Div]
Impsubj(ci) = Σk wk · Subjk(ci)
where each weight wk is normalized such that Σi Imp(ci, r) = 1.
5. Optimization Objectives
The generative engine optimizes for expected answer quality:
maxr E[f(Imp(ci, r), Rel(ci, q, r))]
Content creators, on the other hand, optimize visibility:
maxci Imp(ci, r)
This dual optimization forms the basis of Generative Engine Optimization (GEO).
6. Measuring Visibility Change
After a content update, visibility improvement is defined as:
Improvesi = (Impsi(r') - Impsi(r)) / Impsi(r) × 100
Empirically, factual enrichment and structural clarity yield the highest lifts, confirming that GEs reward grounded and information-dense content rather than keyword repetition.
7. Probabilistic Model of Answer Generation
Each GE stage is a stochastic mapping:
Q1 ∼ p(Q1 | qu; θqr) S ∼ p(S | Q1; θret) Sum ∼ p(Sum | S; θsum) r ∼ p(r | qu, Sum; θresp)
The overall likelihood of producing r given qu is:
p(r | qu) = ΣQ1,S,Sum p(Q1 | qu) p(S | Q1) p(Sum | S) p(r | qu, Sum)
8. DAG Representation
qu → Q1 → S → Sum → r
Each node performs a transformation, and each edge defines a conditional probability distribution.
Critical hyperparameters include fan-out size n, retrieval depth k, summarization ratio α, answer length L, and citation density dc.
9. Why GEO Works
Optimized content affects two conditional probabilities:
Imp(si, r) ∝ P(si ∈ S | qu) × P(si ∈ Ct | si ∈ S)
By improving both retrieval likelihood and synthesis attribution, GEO enables even lower-ranked sources to capture higher visibility in final LLM answers.
10. Multi-Turn Extension
For conversational engines, context history H = ⟨(qt, rt)⟩t=1T conditions the next response:
rT+1 ∼ p(rT+1 | H; θ)
This defines a temporal generative process that continuously updates latent context distributions.
11. Computational Characteristics
If k is the number of retrieved sources and L is the total token length, then inference cost is approximately:
O(k · Lsum + L2)
Summarization is linear in document size, while synthesis scales quadratically with attention, explaining why most engines restrict k ≤ 5 and compress summaries aggressively.
12. Summary
| Component | Role | Mathematical Form |
|---|---|---|
| Query Reformulation | Expand queries | Q1 ∼ p(Q1 | qu) |
| Retrieval | Fetch sources | S ∼ p(S | Q1) |
| Summarization | Compress documents | Sum ∼ p(Sum | S) |
| Synthesis | Generate response | r ∼ p(r | qu, Sum) |
| Impression | Measure visibility | Impwc, Imppwc, Impsubj |
| Optimization | Governs GE utility | maxr E[f(Imp, Rel)] |
Generative engines are probabilistic pipelines that optimize for contextual answer quality under strict latency and memory constraints.
Understanding their mathematical structure is essential to improving your brand's visibility within AI-driven ecosystems.
Want to know more about how Rankly is built to solve your visibility-to-conversion funnel? Schedule a demo today.